1. ATIMA (ATomic Interaction with MAtter) 

2. Stopping power. Energy loss

3. Ranges

4. Energy-loss and ranges straggling 

5. Miscellaneous 

Acknowledgement 

References

Some of the ATIMA subroutines (Version 1.2) have been incorporated into the new version of the LISE code. ATIMA is a user program developed at GSI, which calculates various physical quantities characterizing the slowing-down of protons and heavy ions in matter for specific kinetic energies ranging from 1 keV/u to 500 GeV/u, such as

• stopping power,
• energy loss,
• energy-loss straggling,
• angular straggling,
• range,
• range straggling and others.

ATIMA is available under UNIX. The FORTRAN source of ATIMA has been transformed to C, and was optimized to exclude creating range files for spline procedures. Please report your suggestions for ATIMA via electronic mail to either h.geissel@gsi.de or c.scheidenberger@gsi or h.weick@gsi.de. The web-site of this code is http://www-aix.gsi.de/~scheid/ATIMA1.html.

More details about the physics used in the ATIMA calculations can be found in the following references [Lin96, Sch98, Wei00].
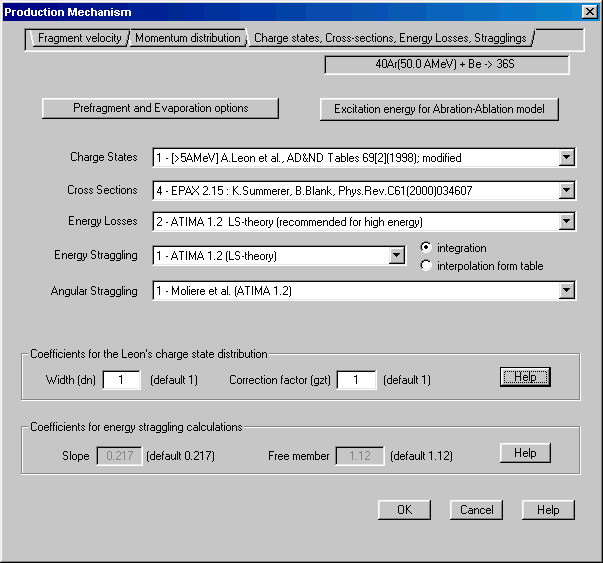
New energy loss and straggling calculation method settings are available via the "Production mechanism" dialog box (see Fig.1).

Four stopping power calculation methods are available in the LISE code (the abbreviation is like in the code):

• 0 - [Hub90],
• 1 - [Zie85],
• 2 - ATIMA 1.2,
• 3 - ATIMA 1.2 without LS-correction".

The "ATIMA 1.2 without LS-correction" method was incorporated to show the influence of the LS-correction. After the various tests for different energies and projectile-target combinations we recommend to use for calculations the following methods:

• At low and intermediate energies (up to 100-300 AMeV), and also for gaseous targets the method "1" [Zie85],
• For high energies (from 150 AMeV and higher) accordingly the method "2" (ATIMA 1.2).

The user can plot energy loss distributions as a function of energy using the "Plot of Fragment Energy Loss (dE/dx) in Target versus Energy" item in the Utilities menu (see Fig.2).

Fig.2. ²⁰⁸Pb energy losses in Be calculated by different methods.

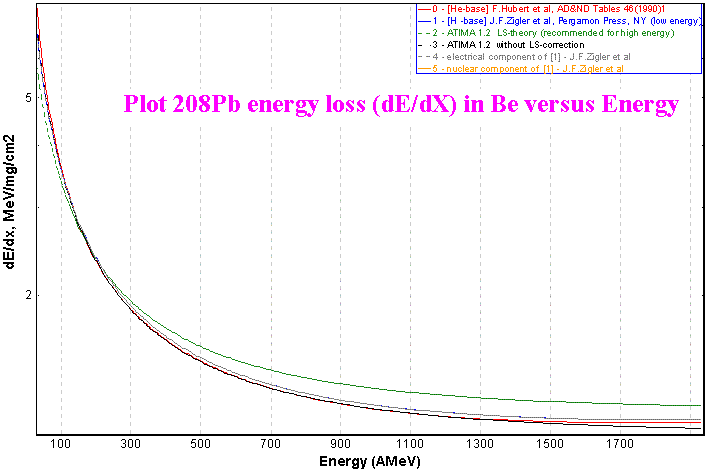
In previous versions the user could create this plot only for a combination beam-target given in the "Projectile" and "Target" menus. In the new version the user can set the necessary combination and choose units (micron or mg/cm²) directly ahead of plot creation via a dialog shown in Fig.3.

Fig.3. The dialog setting the projectile-target combination to plot range or energy loss distributions versus energy.

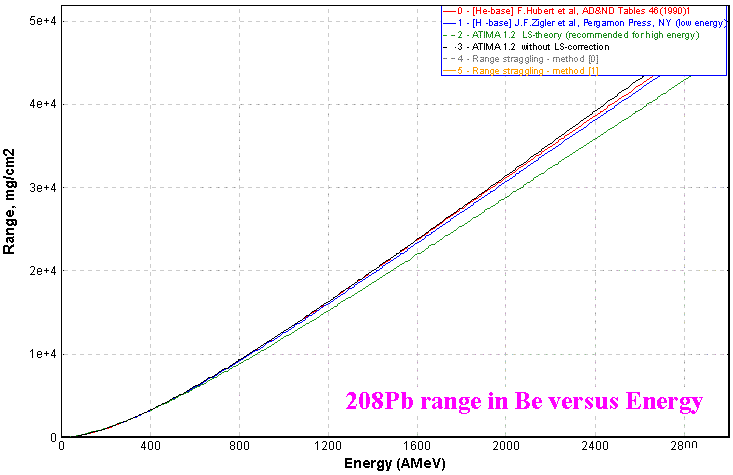
The calculation of energy loss in material is most efficiently performed using a backward interpolation on a table of range calculations. The LISE code is capable to fill ten tables for different combinations (particle, target, calculation method) and to save them in memory in cyclic order. In other words the 11-th combination will be written down in the table instead the first one. This procedure accelerates calculation of run and losses of energy. The user can plot range distributions from energy using the "Plot of Range in Target versus Energy" item in the Utilities menu (see Fig.4).

The LISE code has got a new method for calculating energy-loss straggling (which is based on the ATIMA subroutines) in addition to the [Gui86] method, already existing in the program. The Methods of range straggling calculation were reconsidered. Now the user has two opportunities:

1. Values for range straggling are calculated once from 10 KeV up to 3 GeV/A, and are kept in a table in analogy to the range tables. In LISE this method is referred to as "interpolation from table" (see Fig.1);
2. The second method is called "direct integration": the thickness of the material after which it is necessary to determine the straggling is divided into N parts. The projectile energy is calculated after each such material layer. The final straggling is equal to the square root of the sum of the intermediate values:

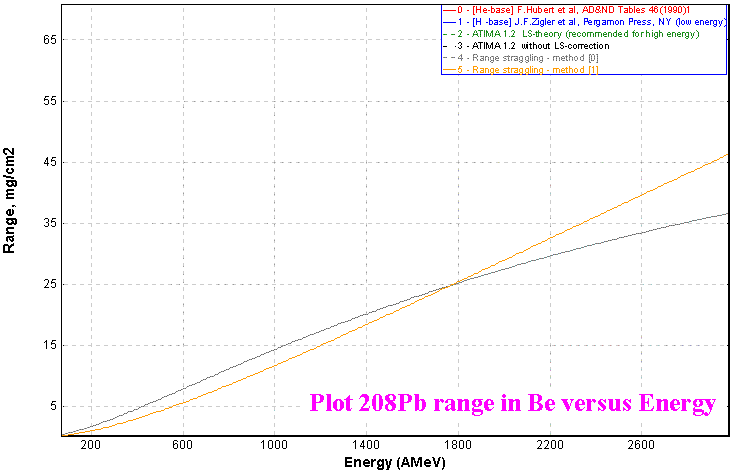
It is recommended to use the ATIMA subroutines to calculate energy-loss straggling using the method "interpolation from table". The user can plot range distributions as a function of energy using the "Plot of Range in Target versus Energy" item in the "Utilities" menu as in the case plot ranges (see Fig.5).

Two methods to calculate the angular straggling are available in the program LISE: [Ann88] and [Par98]. It is recommended to use the [Ann88] method.

Plot "Range in material" subroutines have been reconsidered. In the new version are used table range stragglings instead "integration" method in previous versions.

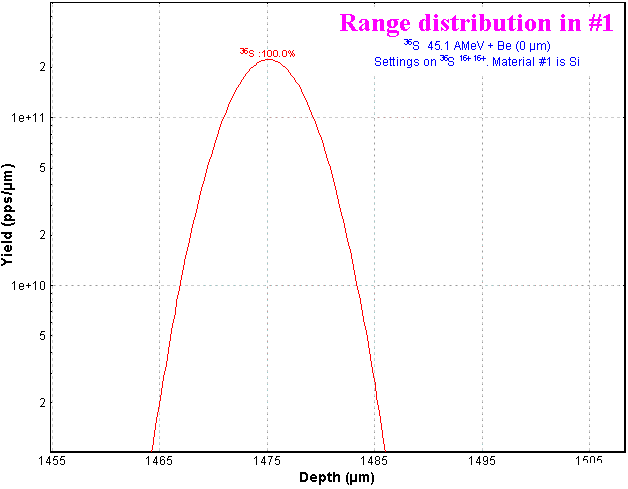
Statistical characteristics of range distribution (Fig.6) are shown in Fig.7. Compare these values with Physical calculator calculations in Fig.8 for the same case.

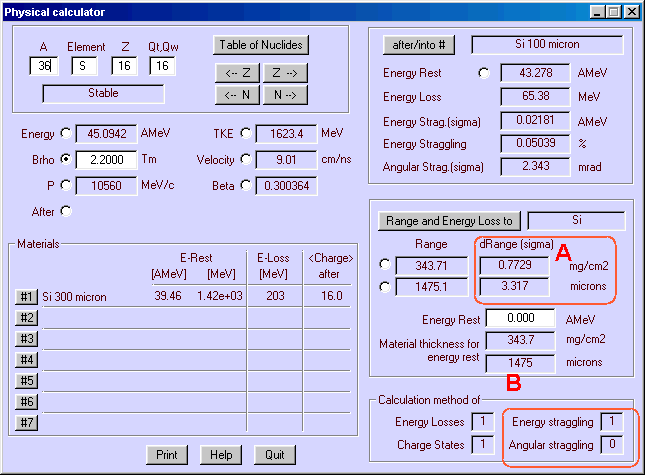
A range straggling is available in the Physical calculator dialog (see A in Fig.8). Methods used to calculate energy loss, straggling, charge states distributions the can observe also (see b in Fig.8)

The LISE program authors thank Dr.H.Weick and Prof.H.Geissel for the help rendered at adaptation of the ATIMA program in our program, and also for the useful remarks at work above the documentation of this version, and also hope for the further cooperation in development of the LISE program.

[Par98] Particle Physics Booklet, 1998, pp.184,185; http://pdg.lbl.gov; (extracted from the Review of Particle Physics C3 (1998) 1).