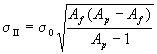 ,
/1/
,
/1/
2. Longitudinal momentum distribution widths
2.1. Systematic of momentum distributions from reactions with relativistic ions of D.J.Morrissey2.2. Heavy ion projectile fragmentation: A reexamination by W.A.Friedman
2.2.1. "Coulomb correction" of Friedman
2.4. Role of intrinsic width in the fragment momentum distributions in heavy ion –collisions (R.H.Tripathi et al.)
2.5. Influence of projectile energy on the reduced width of longitudinal momentum distribution
3.2. Fragment velocity on the basis of surface energy exceed
Fragment momentum distributions measured in relativistic heavy ion collisions are typically observed to be Gaussian shaped. Within the framework of the independent particle model, Goldhaber [GOL74] assumed zero net three-momentum in the nucleus and shoed that the parabolic dependence of the momentum width of the gaussian curve can be obtained:
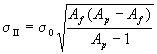 ,
/1/
,
/1/Certainly, that each of models has the advantages and lacks depending on energy and masse of projectile and so on. In the new version of program LISE the user can choose depending on a task necessary to him models from 3 models of fragment velocities and from 3 models of momentum distribution widths or take advantage of new universal "convolution" model.
The reviews of models of momentum distribution widths, velocities of fragments, systematization of the reduced width from energy are submitted to attention of readers in the following chapters.
Also for the new version the Universal parametrization
which allows to avoid a significant part of those lacks (a,d,f,g) that
were inherent in primary statistical model of A.Goldhaber is developed
and adapted in the program.
2. Longitudinal momentum distribution widths
2.1. Systematic of momentum distributions from reactions with relativistic ions of D.J.Morrissey
As the practice shows, many physics use for the description given other distributions, in particular take the width from the empirical systematic of Morrissey [MOR89]:
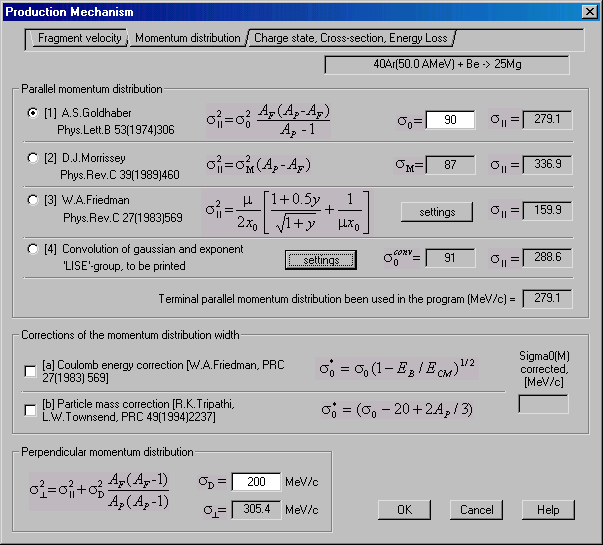
Fig.1. Dialogue "Production mechanism – Momentum distribution"
2.2 Heavy ion projectile fragmentation: A reexamination by W.A.Friedman
Friedman [FRI83] has shown that a model based on the separation energy of fragments from projectile leads to the same functional form as in Goldhaber’s model and a better representation data (at least for light projectiles/O.T./). This model relates the widths of distributions to the separation energies and an absorptive cutoff radius. In this work it is entered a wave function yF-r(r) which describes the relative separation between the observed fragment (F) and the removed portion of the projectile (R) to calculate only outside of the absorption region:
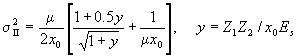 .
/4/
.
/4/| On the other hand, the fragment will be observed if the process leads
to any of its particle-stable excited states. This possibility provides
a range and upper value for Es. The user can choose one
of three possible separation energy: energy on a basis cluster separation
from projectile, excitation energy to the surface exceed, and their sum
(see Fig.2).
However the registered nucleus is consequence of prefragment evaporation of neutrons and light charged particles. Prefragment momentum distribution can differ from a registered fragment considerably. To calculate momentum distribution for prefragment the opportunity of prefragment calculation is entered adjusted for momentum distribution in connection with evaporation. |

Fig.2. Dialogue “Friedman’s momentum distribution width” |
2.2.1 "Coulomb correction" of Friedman
The opportunity of use of the correction for reduced width was added at small energies from distortions due to Coulomb force proposed by W.A.Friedman was incorporated in version 4.7 of the code (see Fig.1):
2.3. Simple parametrization of fragment reduced widths in heavy ion collisions (R.H.Tripathi et al.)
A systematic analysis of the observed reduced widths obtained in relativistic heavy ion fragmentation reactions was used to develop a phenomenological parametrization [TRI94a] of these data:
In work [TRI94b] has been demonstrated comparison of intrinsic widths incorporating correlations in conjunction with dynamical effect with intrinsic widths alone without correlations [GOL74]. They suggested the momentum distribution of the observed fragments depends upon the initial (intrinsic) momentum distribution of the projectile nucleus and upon the momentum transferred by the collision (dynamics):
2.5. Influence of projectile energy on the reduced width of longitudinal momentum distribution
Systematics of reduced widths for projectile like fragments [RAM85,BOR86] have shown abnormal behavior at small energies. From energy 100 AMeV sharp recession of width (see Fig.3) is observed. Different hypotheses were offered, but any of them can not describe a course of a curve at energy of some tens MeV per nucleon. It spoke as the contribution of other mechanisms of reactions, or influence of Coulomb forces. The concept of the contribution of other mechanisms was entered first of all for an explanation low-energetic exponential tail, accompanying gaussian distribution. Coulomb interaction starts to play a role in area below 20 AMeV.
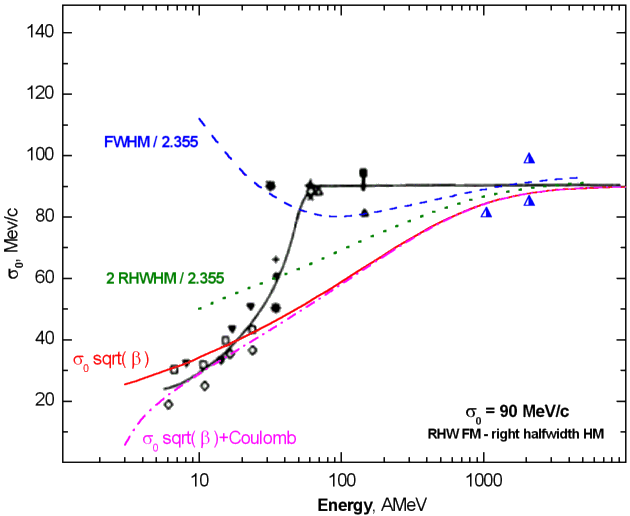
With input of new universal parametrization on the basis of convolution (it will be in more detail submitted in the following chapters) it is possible to explain experimental results. As a result of work on parametrization it was shown, that the width is proportional to a root of velocity. In the figure the given dependence is shown by a red line. The greater consent is achieved for low energies, when to this dependence the Coulomb amendment is added: magenta dash-dot curve. However, how to explain a strong divergence with the data at energies 60-100 AMeV? The answer consists in a method of measurement of width of momentum distribution. At energy 100 AMeV the momentum distribution under the form is very close to gaussian and accordingly experimenters measure full width on maximal height to extract reduced width: a dark blue line received from new universal parametrization. At lower energies however the contribution exponential tail is more appreciable, that is why physics describe distribution by several others. Roughly it can be presented if to consider the right part of distribution as gaussian and to take right halfwidth for calculations of the given width: in figure 3 it is shown by green dotted curve. Two last curves was calculated for reaction 40Ar + Al-> 25Mg.
Momentum distributions of 25Mg in reaction 40Ar(50AMev)+Al
calculated by two methods are presented on Fig.4, where it is well seen
an exponential tail in distribution on the basis of new parametrization.
At initial corrected sigma0 is equal to 43 (![]() )
as a result of convolution it turns out 82 of full width and 63 of right
halfwidth.
)
as a result of convolution it turns out 82 of full width and 63 of right
halfwidth.
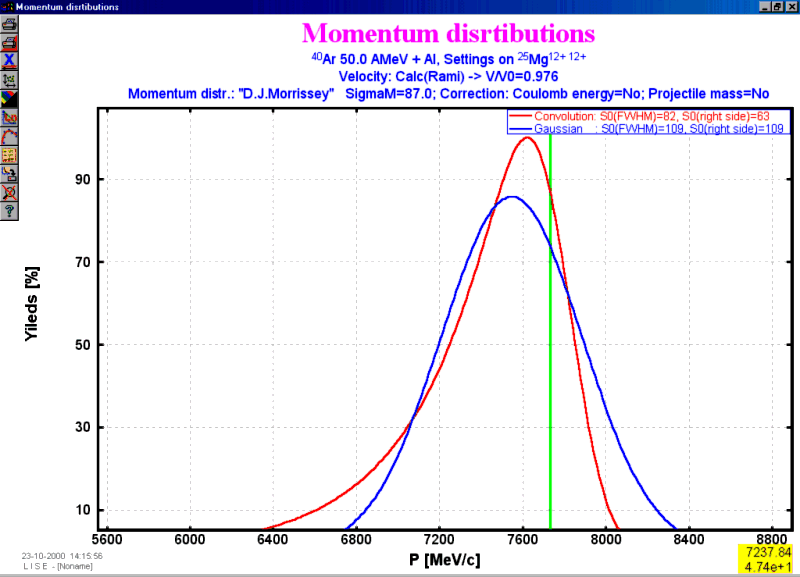
Fig.4. Momentum distributions of 25Mg in reaction 40Ar(50AMev)+Al calculated by two methods: new universal convolution method (red curve), Morrissey parametrization for the momentum width and Rami model for relation of velocities (blue curve).
| As it was already mentioned, velocity of fragmentation reaction products is equal to projectile velocity. In initial versions of the program velocity was considered independent of energy, masses of fragments and an ion of beam. The user in manual entered the relation of velocity of a fragment to a beam. At small energies the relation of velocities is experimentally shown decreases (see Fig.5). Many works show change of this relation due to the contribution of other mechanisms of reactions to an output of products, that accordingly changes the form of momentum distribution. |
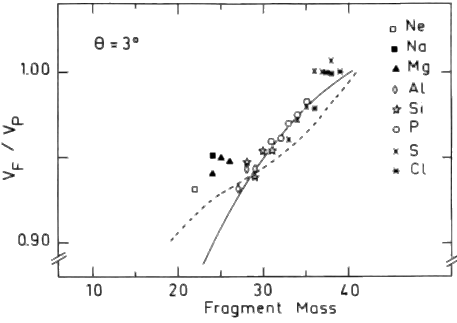 |
3.1. Fragment velocity: removing 8 MeV per ablated nucleon
First estimation [BOR83] of velocity issuing from a fragmentation reaction: if one conjectures that in the fragmentation process the nucleons are removed from the projectile to another and that an average of 8 MeV is required for each (this corresponds to the solid curve in fig.5):
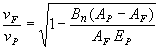 . /9/
. /9/3.2. Fragment velocity on the basis of surface energy exceed
If one assumes that the projectile is sheared in two, then several nucleons bonds have to be broken simultaneously. The number broken can be treated as being proportional to the surface geometry. In the this case [RAM85]:
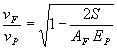 ,
/10/
,
/10/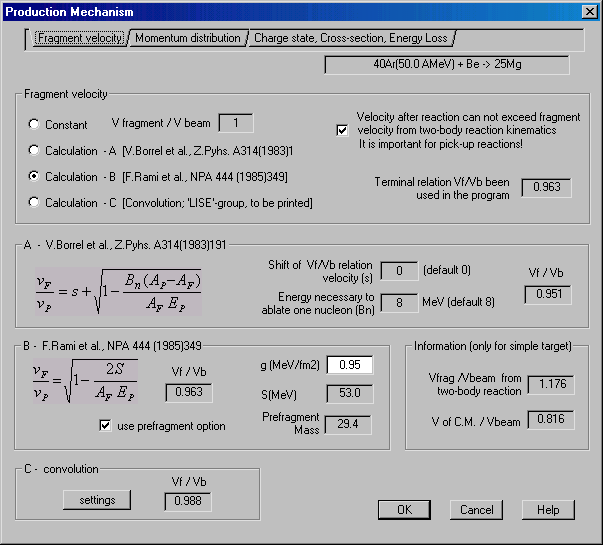
Fig.6. Dialogue "Production mechanism – Fragment
velocity"
Velocities of fragments calculated by different methods in the program
LISE for reactions
40Ar+Al->*Mg (setting nucleus is 25Mg)
are shown in Fig.7.
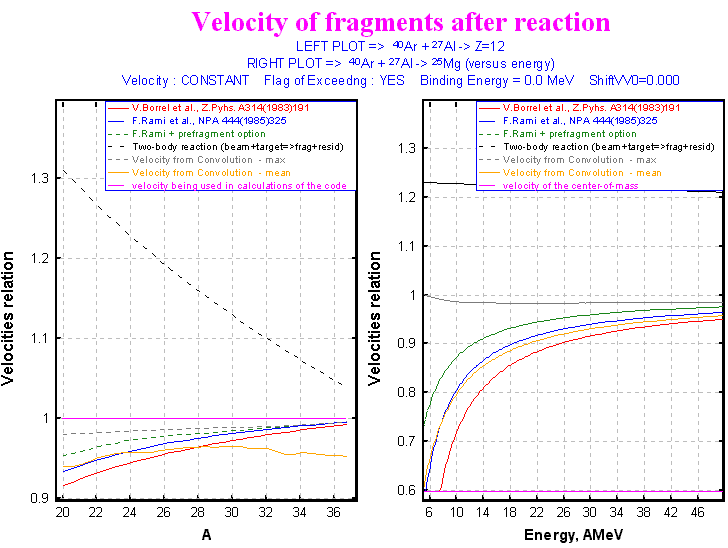
Fig.7. Velocities of fragments calculated by
different methods in the program LISE for reactions
40Ar+Al->*Mg.
Developed in the new version of the program the model of momentum distribution is universal: definition width of distribution depending on beam energy and energy of prefragment excitation, an estimation of the most probable fragment velocity, occurrence a low-energetic exponential tail. Attempt to describe experimental distributions of products of a fragmentation with strongly pronounced gaussian form of beam velocity and with a low-energetic tail at lower energies was undertaken entering convolution between gaussian and exponent. In a basis of model the postulate lays, that energy necessary on division of a projectile on prefragment and participants, and also on prefragment excitation acts ONLY from kinetic energy of projectile. The given assumption lays also in a basis of estimations of speed of a fragment that was described in the previous chapters (equations /9,10/). Obtaining of final distribution needs to be divided into two stages:
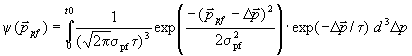 /11/
/11/
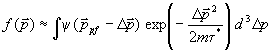 .
/12/
.
/12/
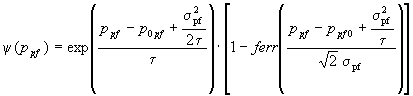 ,
/13/
,
/13/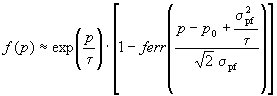 ,
/14/
,
/14/For determination of t the evident form was offered:
![]() .
/17/
.
/17/
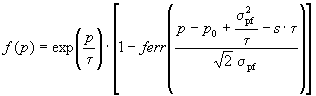 .
/18/
.
/18/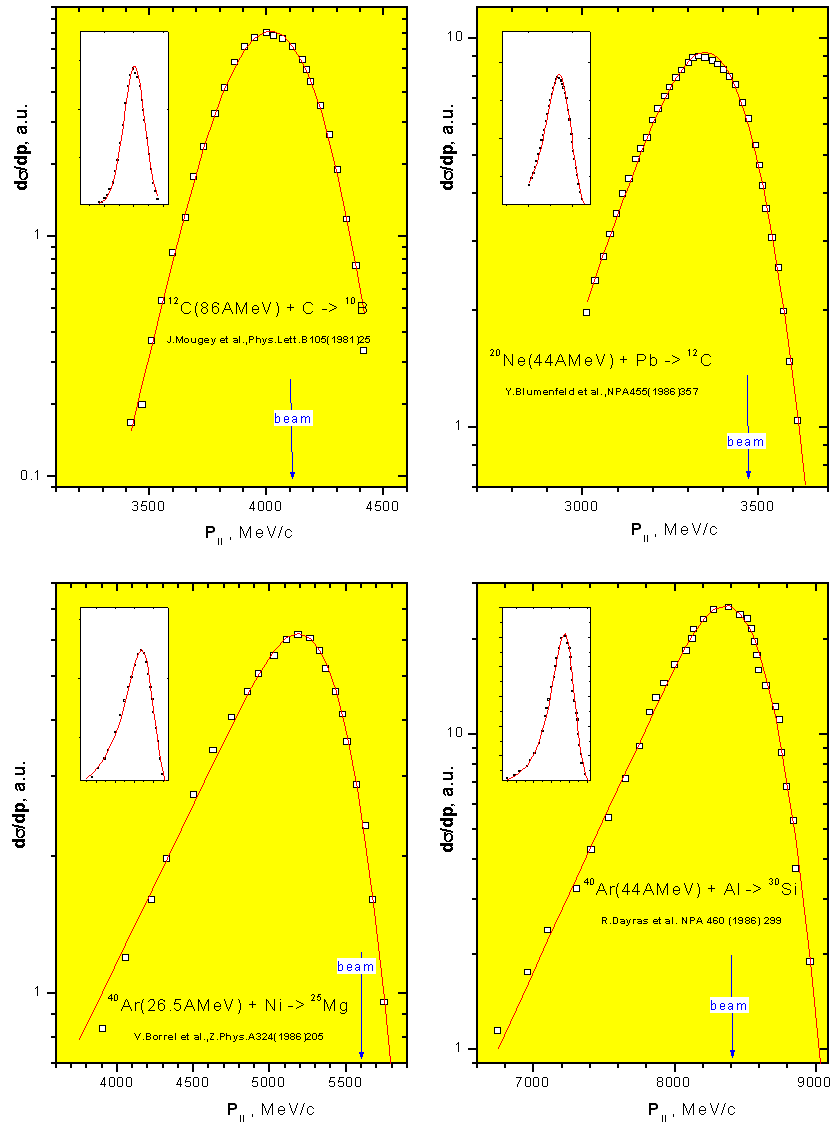
Fig.8. Energy spectra and results of their fit by the formula /18/.
35 spectra from the following works [BOR86,BLU86,DAR86,GRE75,MER86,MOU81,VIY79] were used for fit. In works where distributions from energy were presented, spectra were transformed in momentum distribution in view of the appropriate amendments (see the description to the version 4.5 "Transformation of distributions"). From fit it was received, that value of s0 in expression /17/ is equal to 91,5. Energy spectra and results of their fit by the formula /18/ shown in figure 8.
The experimental data was fitted for three different values of separation energy: energy separation prefragment from projectile, excitation energy of prefragment, and their sum. The best consent was received in a case of "tau" for the second case, for definition of velocity shift the best result was for the third case. All these three opportunities are given in the program (see Fig.9).

Fig.9. Dialogue "Convolution of Gaussian and exponent" called from dialogue"Production mechanism".
[BOR83] V.Borrel et al., Z.Phys.A 314 (1983) 191.
[BOR86] V.Borrel et al., Z.Phys.A 324 (1986) 205.
[BLU86] Y.Blumenfeld et al., Nucl.Phys A455 (1986) 357.
[DAR86] R.Dayras et al., Nucl.Phys. A460 (1986) 299.
[GRE75] D.E.Greiner et al., Prys.Rev.lett. 35 (1975) 152.
[GOL74] A.S.Goldhaber, Phys.Lett. B53 (1974) 306.
[GOS77] J.Gosset et al., Phys.Rev. C16 (1977) 629.
[FRI83] W.A.Friedman, Phys.Rev. C27(1983) 569.
[MOR89] D.J.Morrissey, Phys.Rev. C39 (1989) 460.
[MOU81] J.Mougey et al., Phys.Lett. B105 (1981) 25.
[MER86] M.C.Mermaz et al., Z.Phys. A324 (1986) 217.
[RAM85] F.Rami et al., Nucl.Phys. A444 (1985) 325.
[TRI94a] R.K.Tripathi, L.W.Towsend, Phys.Rev. C49(1994) 2237.
[TRI94b] R.K.Tripathi, L.W.Towsend, F.Khan, Phys.Rev. C49(1994) R1775.
[VIY79] Y.P.Viyogi et al., Phys.Rev.Lett. C42 (1979) 33.