LISE⁺⁺ is the new generation of the LISE¹⁾  code, which allows the creation of a spectrometer through the use of different “blocks”. A “block” can be a dipole (dispersive block), a material (i.e. a given thickness for a detector), a piece of beampipe, etc. The original LISE was restricted to a configuration consisting of two dipoles, a wedge, and a velocity filter. The number of blocks used to create a spectrometer in LISE⁺⁺ is limited by operating memory of your PC and your imagination. The code has an improved interface, new utilities were added, and the spectrometer scheme in the program allows quick editing of blocks (see Last Changes).

  "How to Make Rare Isotope Beams at Home (LISE Package Video Tutorial v.2)"
    @ YouTube by S.Tarasova, 2023

  "Making a ⁶⁴Cr beam with the FRIB Fragment Separator" - YouTube
    by M.Hausmann, 2020 (pdf 725 kB)

  "Making a ⁶⁴Cr beam with the FRIB Fragment Separator"
    by M.Hausmann, 2020 (pptx 724 MB)

  "LISE⁺⁺ tutorial" by D.Bazin, 2003 (pdf 1.3 MB)

  "LISE⁺⁺ tutorial" by P.-L.Tai, 2016 (pdf 3.4 MB)

  "Guide for Using LISE⁺⁺ ..." by T.Ginter, 2007 (pdf 123 kB)

  Conference and Workshop presentations based on the LISE⁺⁺ code development

  "Production of Fast Rare Ion Beams"   lectures at the Euroschool on Exotic Beams including examples of how to use the LISE⁺⁺ code

The program LISE called after the spectrometer of the same name ²⁾   has been developed to calculate the transmission and yields of fragments produced and collected in a fragment separator. Nowadays, projectile fragmentation is being used worldwide in many laboratories to produce Radioactive Nuclear Beams. Being able to predict as well as identify on­line the content of RNBs is therefore of prime importance. This has guided the definitions of the main purposes and characteristics of the program:

  Predict fragment separator settings to obtain a specific RNB;
  Predict the intensity and purity of the chosen RNB;
  Simulate identification plots to be compared on­line (see Fig.1);
  Provide a highly user­friendly environment;
  Possibility to configure the program for different fragment separators.

Fig.1. Plot of transmitted fragments after magnetic rigidity filtering. The axes are the energy loss for the ordinate and the time-of-flight for the abscissa. This plot and subsequent identification plots are produced by a Monte-Carlo generator to better mimic the experimental spectra observed on-line.

A statistical model ^3,4) is used to determine the momentum and angular phase space distributions of the projectile fragments. The average fragment velocity can be set to a constant value or can be calculated from the expressions given in the code. The cross sections are calculated according to a global parameterization EPAX ⁵⁾ with no energy dependence. Four different built-in parameterizations ^5,6) of cross sections based on the EPAX model and Geometrical Abrasion-Ablation model are available. It is also possible to directly enter the cross section for a given reaction, provided it was previously measured or calculated by more sophisticated codes. Once a cross section is manually entered in the program it is automatically saved with the results of calculations.

The determination of the equilibrium charge state distribution of an ion beam after passing through material can be calculated according to three different parameterizations ^7-9).The calculation of charge state distributions and their corresponding transmissions can be enabled or disabled by selecting the Charge States option. In case it is enabled, the charge states of the fragment of interest have to be specified after the target and the wedge.

The calculation of energy loss and energy straggling is crucial for deducing magnetic rigidities, transmission of fragments and their ranges in detectors. Two energy loss calculation methods are available ^10,11). Energy losses are calculated for atomic numbers (1 =< Z =< 130) and energies from 10 keV in materials from Hydrogen up to Uranium. The calculation of energy loss in gas and composite materials is also included.

built-in Energy loss, Time-of-Flight, Position, Angular, Charge, Cross-Section distribution plots and dE-E, dE-TOF, Z-A/Q and dE-X two-dimensional plots allow to visualize the results of the program calculations. An application of transport integral ¹²⁾ lies in the basis of fast calculations of the program for the estimation of temporary evolution of distributions of phase space.

In 1998 the program has undergone a number of serious changes and has been adapted to the environment of "Windows"

   Being adapted to the 32-bit operating system «Windows» the program has received an improved interface with which the user gets all opportunities of the given operating system (work in several windows, drivers of a seal etc.);

   There appeared an opportunity to choose the parameterization of fragmentation cross-sections and model the charge distributions of ions;

   built-in database of nuclides has been added. It is possible to see a transmission of a given isotope, its characteristics and energy after second dipole clicking on an isotope of interest in the table of nuclides by the right button of the mouse;

   The optical parameters of the spectrometer are entered as transport matrices that are more convenient. Initial angular, spatial and energy emittances of beam are used;

   The new dipole after the Wien filter of velocities has been added;

   There appeared an opportunity to choose a degrader profile (achromatic, monochromatic, homogeneous, user-defined) in the intermediate dispersive focal plane.

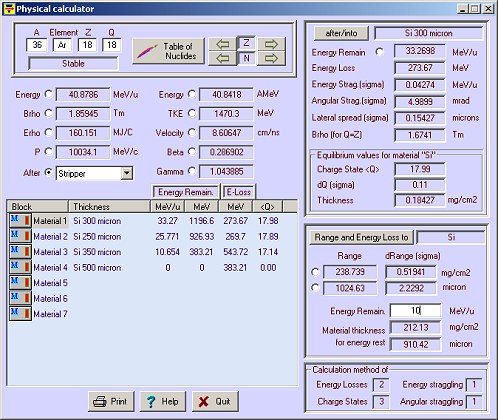
Fig.2. Physical calculator window showing various calculations performed for the nucleus ²⁴O. The energy can be entered not only by the different parameters such as magnetic rigidity, velocity or momentum (radio buttons on the left), but also by specifying either an energy after a given material (top right) or the total range (bottom right).

In addition, several general purpose tools such as a physical parameters calculator (see Fig.2), a scattering calculator, a database of nuclei properties, and relativistic two body kinematics calculations make it also attractive in experiments where radioactive beams are not involved. Most of the options available in the program are well documented in an on­line help. The constant improvements of the code based on the user's remarks has brought its high flexibility and made it well adaptive to almost any nuclear physics experiment using magnetic and/or electrostatic separation devices. With the advent of the World Wide Web, it has become very easy to maintain and update the program, and it can now be freely downloaded and installed at the addresses:

References